При изучении школьного курса геометрии в двумерном пространстве большое время уделяют рассмотрению поведения прямых. Когда же переходят к изучению стереометрии в старших классах, то на первый план выходят темы плоскостей и прямых в пространстве. Данная статья посвящена одному из таких вопросов. А именно теме вычисления между плоскостями и прямыми углов и расстояний.
Прямая на плоскости и способы ее задавания
Чтобы с успехом решать задачи вычисления между прямыми и плоскостями углов и расстояний, необходимо научиться математически задавать эти геометрические объекты, а также овладеть методами работы с соответствующими уравнениями. Начнем с задавания прямых на плоскости.
Каждый школьник знает следующую формулу:
y = k*x + b
Работать с ней достаточно удобно в двумерном пространстве. Ее легко использовать, чтобы начертить прямую в прямоугольной системе координат. Кроме того, знание коэффициента k для каждой из них позволяет сказать, будут ли они параллельны, или же они пересекаются (для параллельных их коэффициенты k равны).
Если записать приведенное выражение в несколько ином виде, то получится формула общего типа для прямой. Ее форма следующая:
A*x + B*y + C = 0
Очевидно, что с помощью простых преобразований можно получить из нее первое выражение.
Записанные формулы можно применять также для вычисления угла пересечения прямых. Однако для этого необходимо провести ряд преобразований, что является неудобным. Поэтому, когда в задаче требуется найти какой-либо угол, предпочтительнее пользоваться векторной формой представления прямой. Ее вид можно записать так:
(x; y) = (x0; y0) + λ*(a; b)
В этом равенстве координаты икс и игрек с нулевыми индексами описывают положение некоторой точки, через которую прямая проходит. Значения a и b являются координатами вектора, лежащего на ней. Он может быть направлен как в одну сторону прямой, так и в другую, прямая от этого не изменяется. Указанный вектор принято называть направляющим, поскольку он однозначно определяет распространение прямой на плоскости. Лямбда λ - это параметр, который принимает произвольное значение из множества действительных чисел.
Обращаем внимание, что векторная форма записи тем и замечательна, что явно содержит направленный отрезок прямой, координаты которого используются для определения угла между двумя прямыми на плоскости.
Прямая в трехмерном пространстве
В пространстве, описываемом тремя координатными осями, прямая задается в общем виде как пересечение плоскостей. Здесь же, учитывая тему статьи, рассмотрим только уравнение векторное. Оно подобно таковому для плоского случая, но с добавлением третьей координаты:
(x; y; z) = (x0; y0; z0) + λ*(a; b; c)
При решении задач это выражение удобно раскрывать и применять в параметрическом виде:
x = x0 + λ*a;y = y0 + λ*b;z = z0 + λ*c
Отметим, что значение параметра λ хотя и является произвольным, но будет зависимым для всех трех равенств.
Описание плоскости
Как и для прямой, для плоскости тоже существует ряд способов ее определения. Рассмотрим лишь два из них, которые важно знать, чтобы уметь решать задачи на практике.
Первый способ задания заключается в приведении уравнения общего типа. Оно аналогично соответствующему выражению для прямой в двумерном случае:
A*x + B*y + C*z + D = 0
Совокупность первых трех коэффициентов - это координаты направляющего вектора для этой плоскости. Как правило, его обозначают символом n¯, то есть:
n¯ = (A; B; C)
Четвертый коэффициент D определяет расстояние, на которое отстоят друг от друга параллельные плоскости, имеющие первые три одинаковых коэффициента.
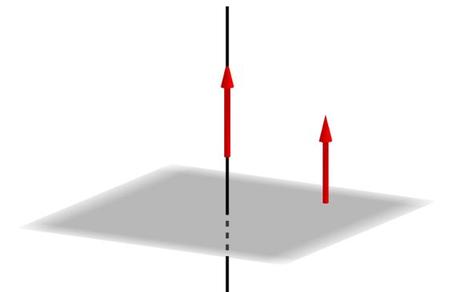
Поскольку вектор n¯ лежит на нормали к плоскости, то он перпендикулярен абсолютно любому вектору и прямой, построенным на ее произвольных двух точках. Знание координат n¯ является ключевым при определении между прямыми и плоскостями углов.
Второй способ определения плоскости - это векторно-параметрическая форма уравнения. Она записывается таким образом:
(x; y; z) = (x0; y0; z0) + λ*(a1; b1; c1) + γ*(a2; b2; c2)
Это равенство отражает тот факт, что две прямые однозначно задают в пространстве плоскость. Здесь второй и третий члены обозначают два направляющих вектора для произвольных прямых, принадлежащих плоскости.
Нормальный вектор n¯ не содержится в явном виде для этой формы записи, однако его легко вычислить:
n¯ = [(a1; b1; c1)*(a2; b2; c2)]
Угол между прямыми
Если известны векторные равенства для каждой из прямых, то рассчитать между ними угол не представляет никакого труда. Для этого нужно лишь использовать свойства скалярного произведения для направляющих отрезков прямых. Если направляющие вектора обозначить символами v¯ и u¯, тогда искомая формула примет вид:
α = arccos(|(v¯*u¯)|/(|v¯|*|u¯|))
Поскольку в случае пересечения прямых образуется две пары равных углов, то за истинный угол между ними принимают острый. По этой причине в формуле присутствует знак модуля в числителе.
Эта формула для двумерного случая справедлива всегда. При этом полученное значение 0o говорит, что прямые не пересекаются, а являются параллельными.
Что касается случая в пространстве, то помимо расчета по формуле необходимо проводить дополнительные вычисления. Они связаны с нахождением точки пересечения рассматриваемых объектов. Дело в том, что в пространстве можно получить конечное значение угла α, но прямые при этом пересекаться не будут, поскольку могут являться скрещивающимися.
Плоскость, прямая и формула угла их пересечения
Чтобы найти угол между прямой и плоскостью, достаточно знать уравнение для каждого из этих объектов. Углом между ними называется угол двух пересекающихся прямых, одна из которых - исходная, а другая принадлежит плоскости и является проекцией исходной прямой на нее. На рисунке ниже показана плоскость, которую пересекает прямая под углом α.
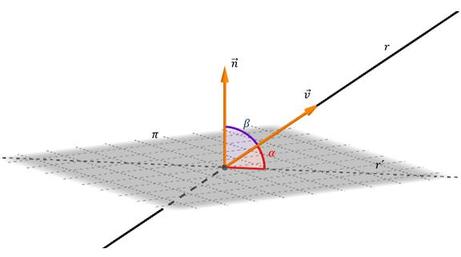
Если направляющий для прямой вектор обозначить v¯, а нормаль плоскости - n¯ (см. рис.), то вычисление угла α производится по формуле:
α = arcsin(|(v¯*n¯)|/(|v¯|*|n¯|))
Заметим, что в этой формуле, в отличие от аналогичного выражения для двух пересекающихся прямых, используется функция арксинуса, а не арккосинуса.
Расстояние между прямыми на плоскости и плоскостью и прямой в пространстве
Для расчета расстояния между рассматриваемыми объектами в геометрии существует набор формул. Применение того или иного выражения из него зависит от того, в каком виде задана плоскость и прямая.
Если две прямые заданы в общем виде на плоскости, то расстояние между ними можно рассчитать так:
d = |A*x1 + B*y1 + C|/√(A2+B2)
Здесь x1 и y1 являются координатами произвольной точки на одной прямой, а коэффициенты A, B, C взяты для другой прямой. Данная формула справедлива, если прямые параллельны друг другу. Если они пересекаются, то расстояние равно нулю.
Расстояние между прямой и пересекающей ее плоскостью равно нулю. Если же прямая параллельна плоскости, тогда соответствующая дистанция вычисляется так:
d = |A*x1 + B*y1 + C*z1 + D|/√(A2+B2+C2)
Где координаты принадлежат произвольной точке на прямой.
Задача: определить между прямой и плоскостью угол
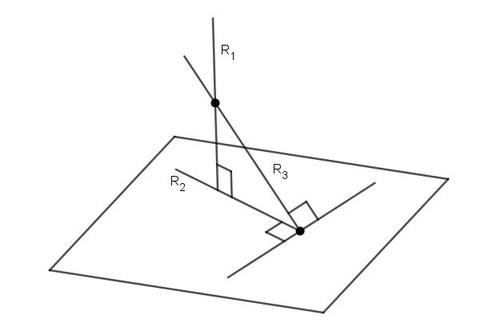
Даны прямая и плоскость:
(x; y; z) = (1 ; 2; 0 ) + λ*(-1; 1; 4);-5*x + y - 3 = 0
Чему равен угол между прямой и плоскостью?
Выпишем направляющие вектора v¯ и n¯:
v¯ = (-1; 1; 4);n¯ = (-5; 1; 0)
Подставим их в соответствующую формулу для α, получаем:
α = arcsin(|5+1+0|/(√18*√26)) ≈ 16,1o
Задача: найти расстояние между прямыми
Заданы два уравнения прямых в двумерном пространстве:
y = 3*x - 1;y = 3*x + 3
Чему равно расстояние между ними?
Поскольку коэффициенты k для обоих объектов одинаковые (равны 3), то имеет место случай параллельных прямых.
Чтобы рассчитать расстояние между ними, возьмем произвольную точку первой прямой, а уравнение второй перепишем в общем виде, имеем:
координаты точки (0; -1);3*x - y + 3 = 0, то есть A = 3, B = -1, C = 3
Теперь эти значения можно подставить в соответствующую формулу:
d = |3*0 -1*(-1) + 3|/√(9 +1 ) = 4/√10 ≈ 1,265
Ответ получен в единицах данной координатной системы.



А ЧТО ВЫ ДУМАЕТЕ ОБ ЭТОМ?